Oskar’s Matchboxes is another puzzle designed by Oskar Van Deventer. This seems like a simple enough puzzle, where five matchboxes have their sleeves and drawers attached at interesting angles to create five unique pieces. The goal is to close all five matchboxes. Have a look here for Brian’s review.
I recently won a copy of Oskar’s Matchboxes, made by Eric Fuller in 2010, on the recent Cubic Dissection Marketplace auction. This is a beautifully made version using (as best I can tell) Mahogany and Maple. Overall, the puzzle is approximately 3.5″ in size, making for a very compact version.
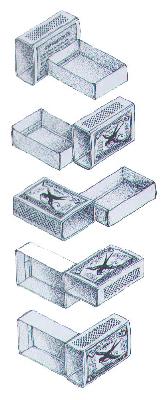
The diagram on the right shows how each of the matchboxes should be attached. The dimensions of the boxes are fairly important, they need to be on a 3:2:1 scale in order for the puzzle to work correctly. There have been a number of versions of the puzzle made, including short runs by Trevor Wood, Tom Lensch and Eric Fuller. Each of those has a different appearance as the creator can make the boxes in whatever style they desire, as long as it remains inside the dimensions listed. Recently Philos Games has started creating a mass manufactured version of the puzzle which you can buy directly or at Puzzle Master or Amazon.
When I received this puzzle, Eric’s description states that there are two solutions, however I was aware that Trevor Wood claims there are three solutions. I set myself a challenge to find all three solutions or prove that there were only two. When I received the puzzle, it was already in the solved state, so I took it apart, shuffled the pieces and starting trying to put it back together. After about an hour I had the five boxes back together. This is a tough puzzle, and is very easy to get lost trying to solve it. A systematic approach will serve you best when trying to solve this, as randomly lifting pieces is unlikely to be successful.
With one solution found, I started looking for the others. After another 15 minutes, I found a way to change the location of only one piece and still solve the puzzle. Having done this, I had to take photographs of the two solutions to prove to myself that they were indeed different. The two solutions are mirror images of each other, so easy to miss that they are different. (You can click this link to see all solutions)
So two down. Could I find the third? As it happens, I had come across the third solution while trying to solve the puzzle for the first time, however it is not possible to create this third solution with Eric’s version of the puzzle. At this point, you might think I’d give up and accept that it wasn’t possible to create the third solution. Well, I’m not the sort of person that gives up. I wanted to create a version where all three solutions were possible. As Trevor Wood points out, the dimensions of the puzzle, and exact placement of the drawers is required to be able to create all three solutions.
One thing that made me want to create my own version was this image of the Philos Puzzle in the solved state (thanks to Brian Pletcher for the image). If you look at the image on the Puzzle Master site, you’ll see that it is solved in the same way as I have it solved, but here is a completely different solution, this one much flatter than the two possible using Eric’s version!
Off to the store I went to buy some matchboxes. (As a side note, you have no idea how difficult it seems to be to buy a standard matchbox in San Jose!) With a pack of 10 matchboxes in my hand I took out my tape, and started joining the sleeves and drawers together to match the diagram above, while creating an ever increasing pile of matches on my workbench.
The result speaks for itself (see the link below as I have not included the solutions by default so you can discover them for yourself!). The third solution which was not possible with the very high quality version from Eric Fuller.
If you want to see all three solutions, click here, and browse the images. Note, these won’t appear if you click any of the other images so if you don’t want to compare the solutions, you’re not going to be exposed to them accidentally.
As an additional challenge, try putting the matches back into the boxes when you solve the puzzle. After all, they are matchboxes, and should still be able to store the matches. I went ahead and did just that, and realised that the puzzle becomes harder. Given the interesting orientation of the drawers, the order in which you close them now becomes even more important, as it;s not possible to put them together in all orders since the matches will fall out (unless you have 4 hands!)
This is a fun project, and fairly simple as long as you get matchboxes with the correct scale. Have a go, and let me know how you get on. Alternatively, pick up a copy of the Philos version and have a go at finding all three solutions yourself.